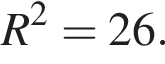1. Задание № 31 

Сложность: I
Классификатор алгебры: 13\.1\. Область определения функции
Область определения функции
i
Функция 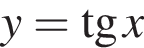 не определена в точке:
не определена в точке:
1) 
2) 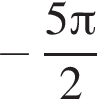
3) 
4) 
5) 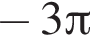
Решение. Функция 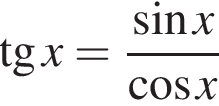 не определена, когда
не определена, когда 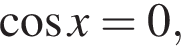 т. е. при
т. е. при 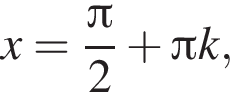 где
где ![]() Таким образом, она не определена в точке
Таким образом, она не определена в точке ![]()
Правильный ответ указан под номером 2.
Ответ: 2
31
2
Сложность: I
Классификатор алгебры: 13\.1\. Область определения функции
 см2.
см2.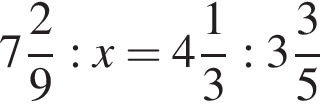 — верная пропорция, то число x равно:
— верная пропорция, то число x равно: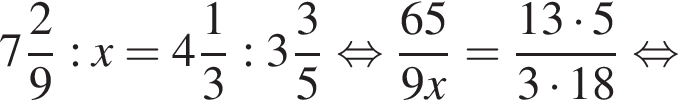
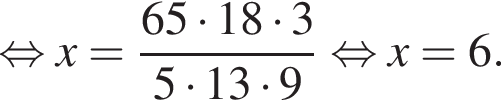
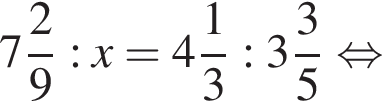
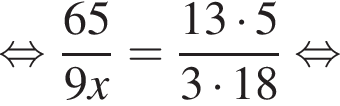
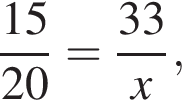 где x — неизвестное число.
где x — неизвестное число.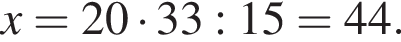
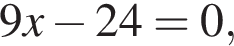 то
то 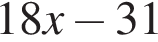 равно:
равно: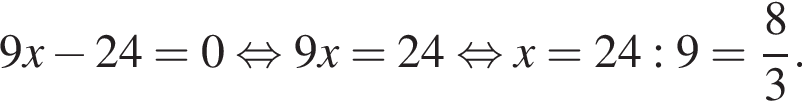
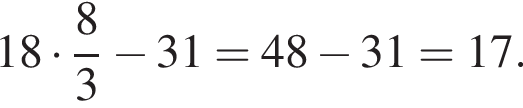
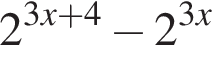 имеет вид:
имеет вид: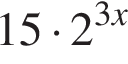
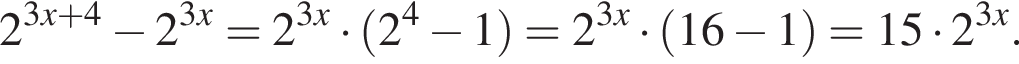
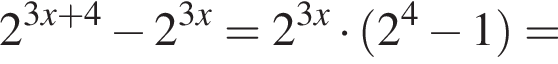
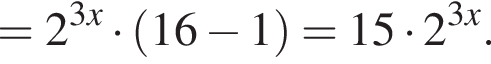
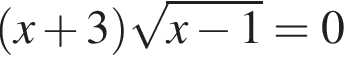 равна:
равна: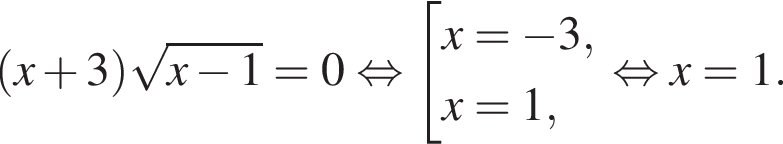
 Тогда:
Тогда: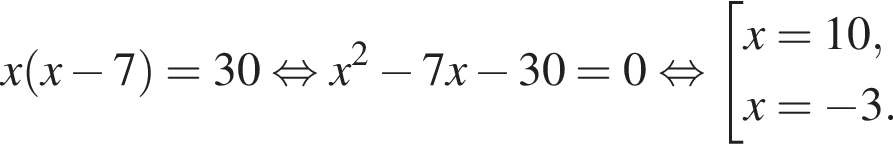
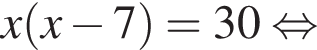
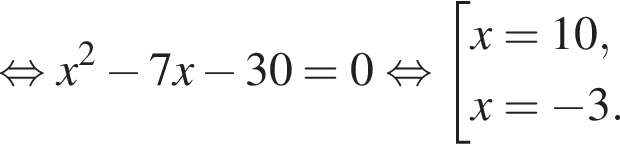
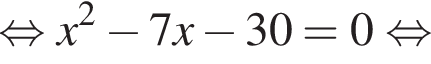
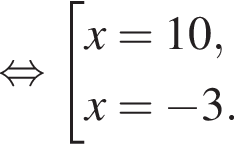
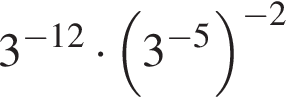 равно:
равно: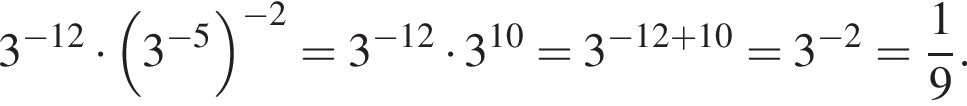
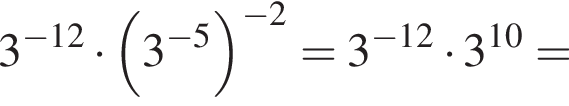
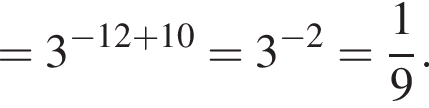
 так как это прямоугольник. Тогда для площади боковой поверхности имеем:
так как это прямоугольник. Тогда для площади боковой поверхности имеем:
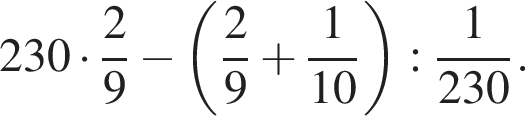
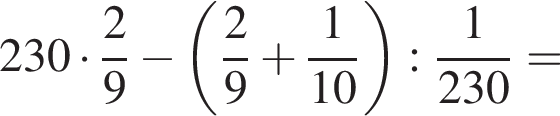
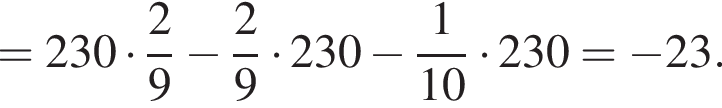
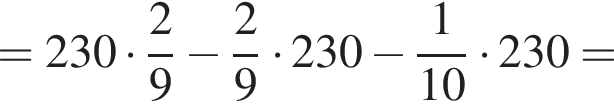
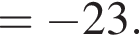
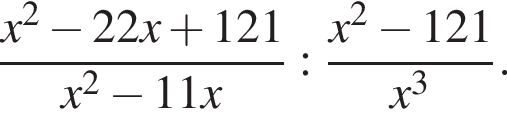
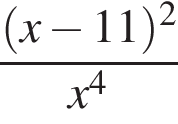
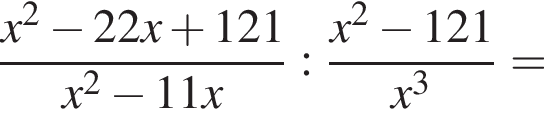
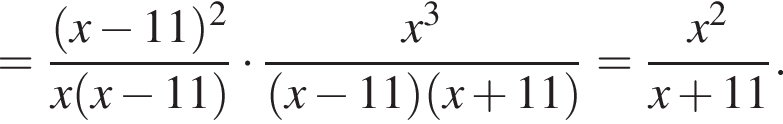
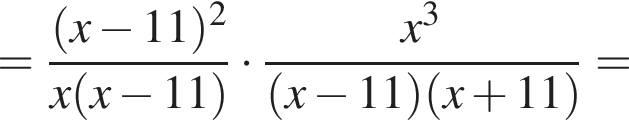
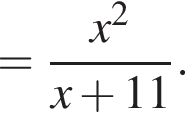
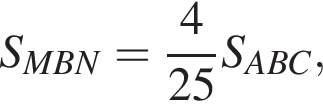 а тогда
а тогда 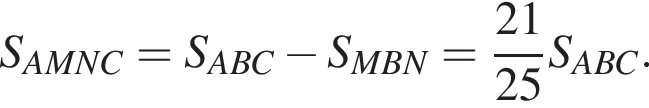
 и
и 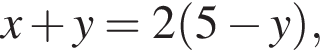 равна:
равна: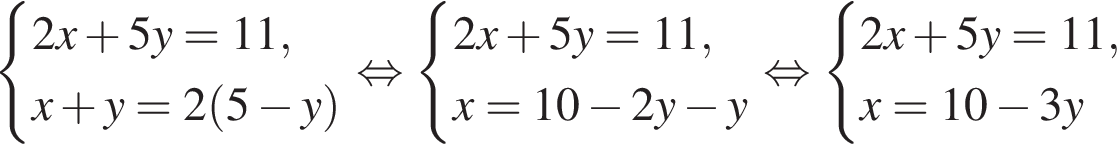
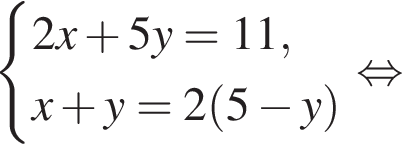
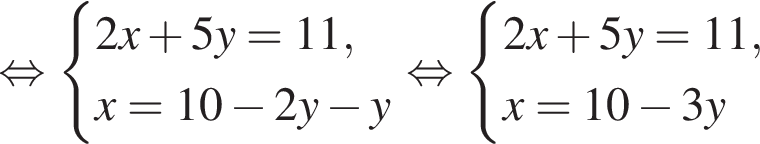
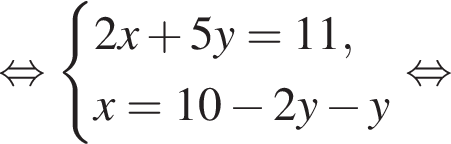
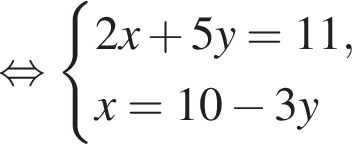
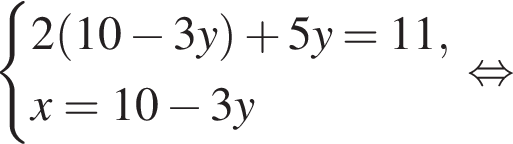
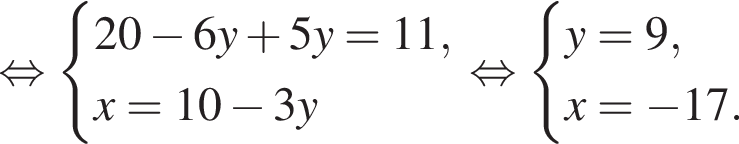
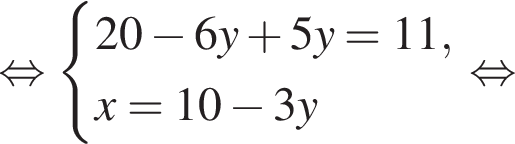
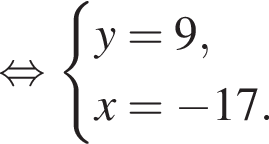
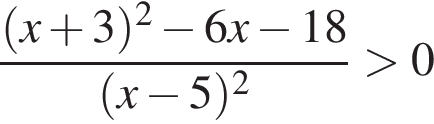 на промежутке
на промежутке 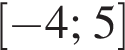 равно:
равно: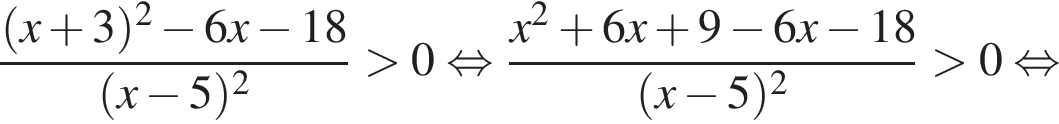
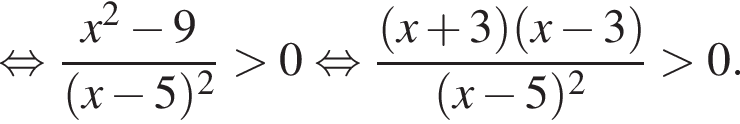
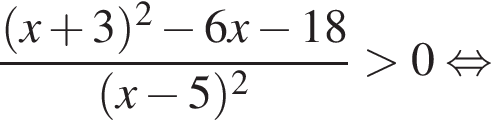
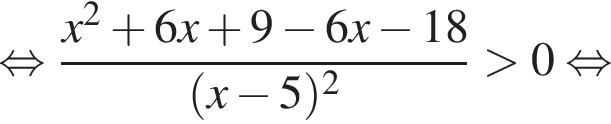
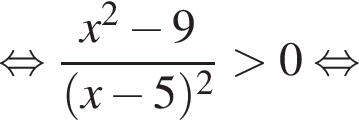
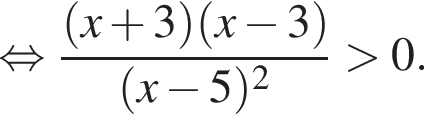
 Корни знаменателя
Корни знаменателя 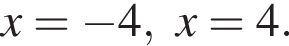 Следовательно, существует только 2 целых решения.
Следовательно, существует только 2 целых решения. 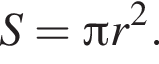 Следовательно, радиус круга равен:
Следовательно, радиус круга равен: 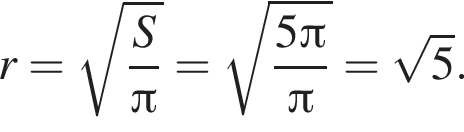 Площадь ромба равна произведению высоты на его сторону:
Площадь ромба равна произведению высоты на его сторону:  Тогда:
Тогда: 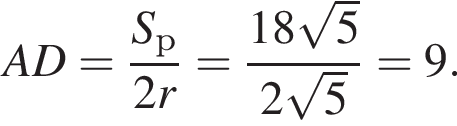
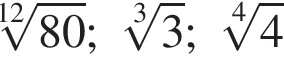 в порядке возрастания.
в порядке возрастания.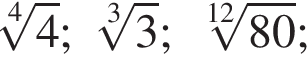
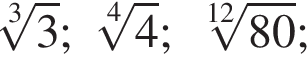
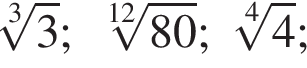
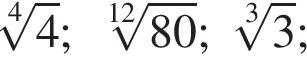
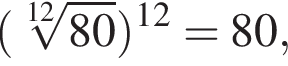
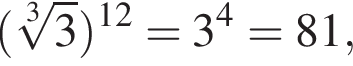

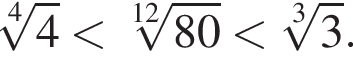


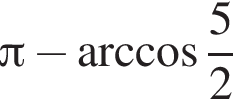
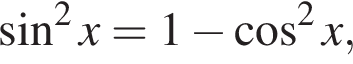 получим:
получим: 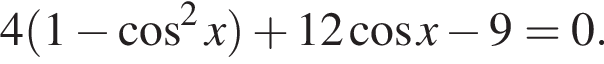 Сделаем замену
Сделаем замену 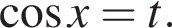 Решим уравнение:
Решим уравнение: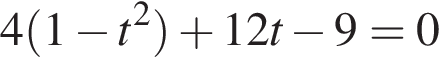
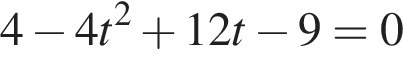
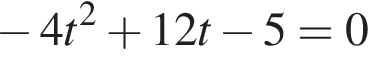
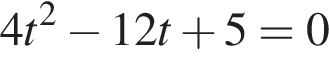
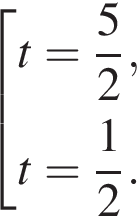
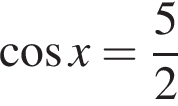 или
или 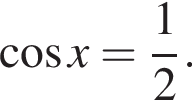 Первое уравнение решений не имеет, поскольку
Первое уравнение решений не имеет, поскольку 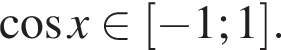 Рассмотрим второе уравнение:
Рассмотрим второе уравнение: 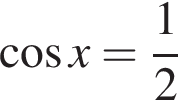
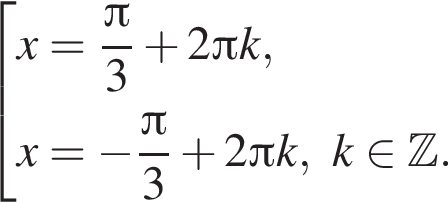
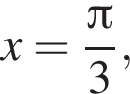 он указан под номером 3.
он указан под номером 3.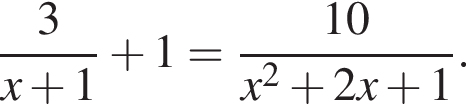
 :
: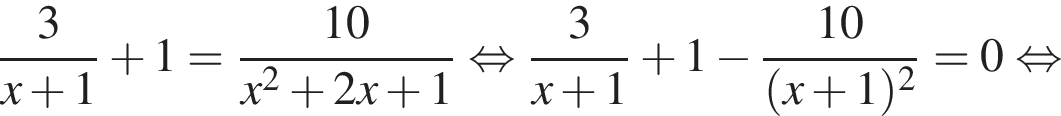
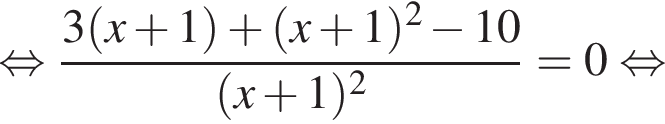
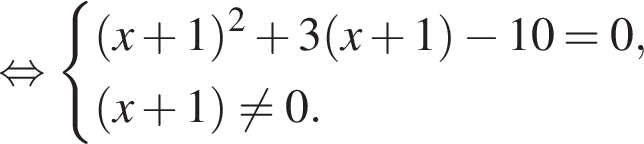
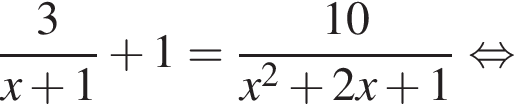
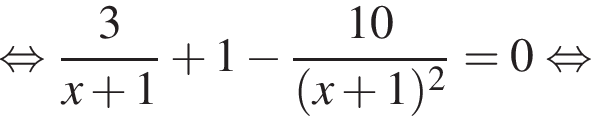
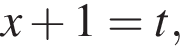 тогда:
тогда: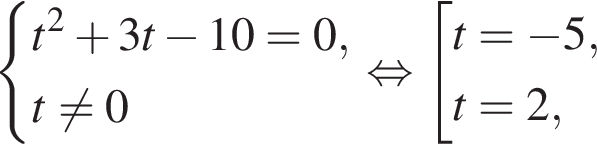
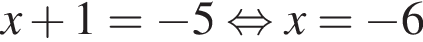 или
или 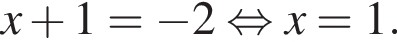

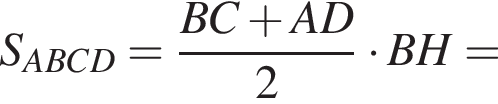
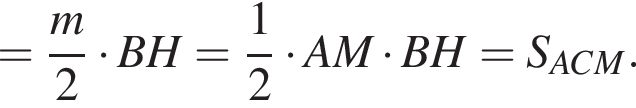
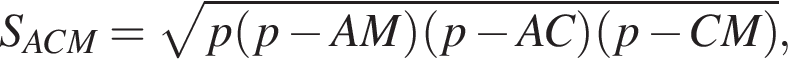 где p — полупериметр треугольника ACM, который равен:
где p — полупериметр треугольника ACM, который равен: 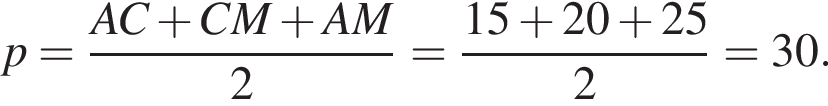

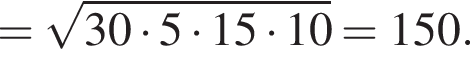
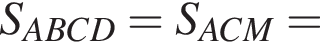

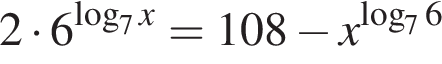 равна ...
равна ...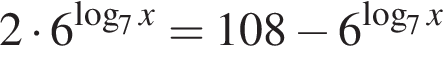
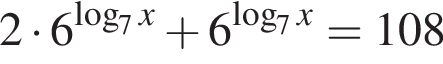
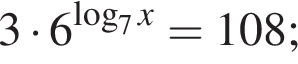
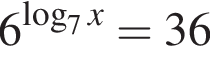
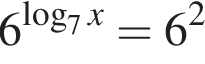
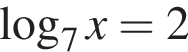
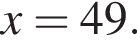
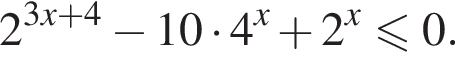
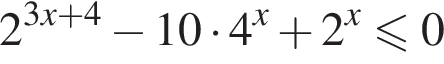
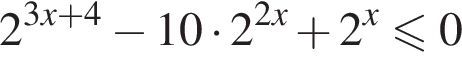
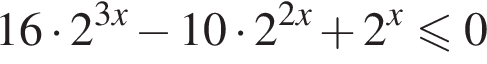
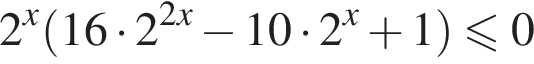
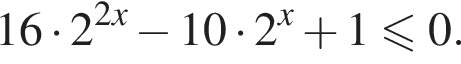
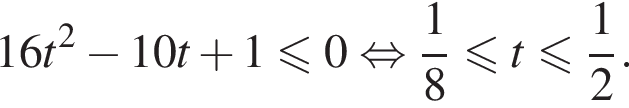
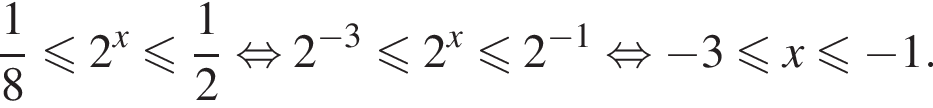
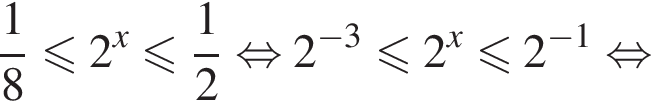

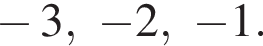 Их сумма равна −6.
Их сумма равна −6.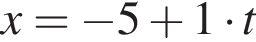 (м) и
(м) и 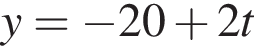 (м).
(м).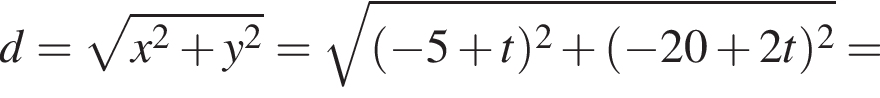
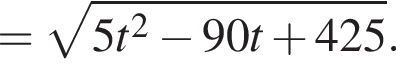
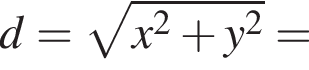
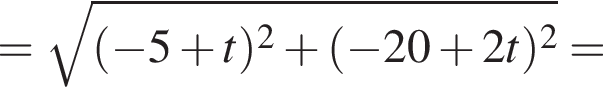
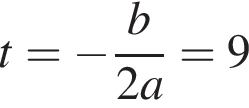 и в этой точке положительно:
и в этой точке положительно: 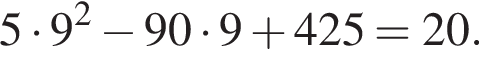 Таким образом, при
Таким образом, при 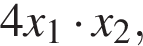 где x1, x2 — абсциссы точек пересечения параболы и горизонтальной прямой (см. рис.).
где x1, x2 — абсциссы точек пересечения параболы и горизонтальной прямой (см. рис.).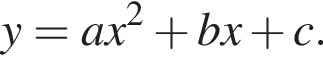 На рисунке изображена парабола с ветвями, направленными вверх, следовательно,
На рисунке изображена парабола с ветвями, направленными вверх, следовательно, 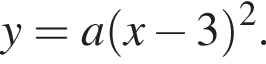 Для того, чтобы найти a, подставим в уравнение параболы точку (2;1), через которую данная парабола проходит:
Для того, чтобы найти a, подставим в уравнение параболы точку (2;1), через которую данная парабола проходит: 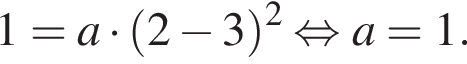 Таким образом, изображённая на графике парабола задается уравнением
Таким образом, изображённая на графике парабола задается уравнением 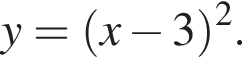
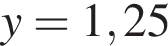 :
: 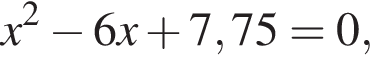 откуда по теореме Виета
откуда по теореме Виета 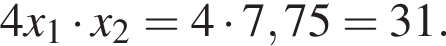
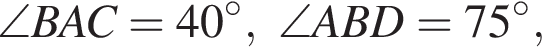 то градусная мера между прямыми AB и CD равна ...
то градусная мера между прямыми AB и CD равна ...

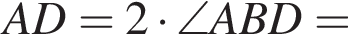

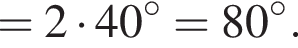
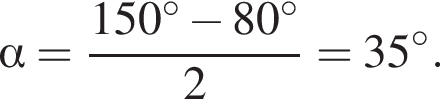
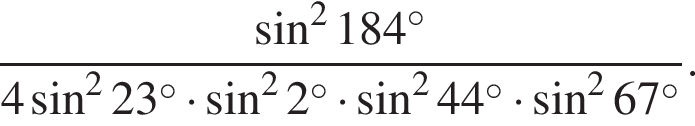
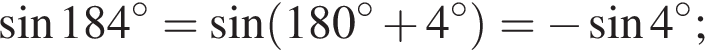

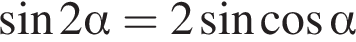 :
:
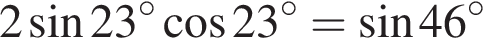
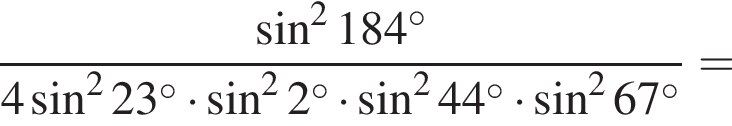
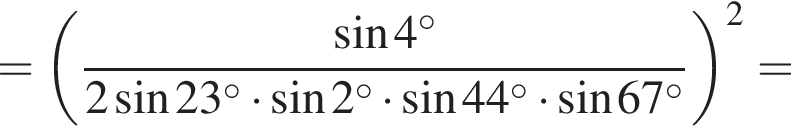
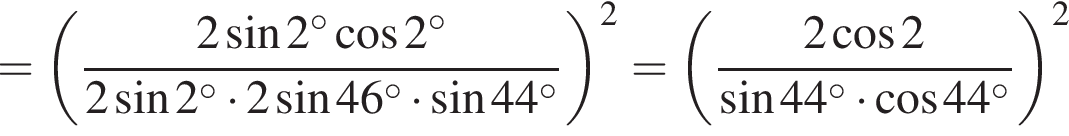
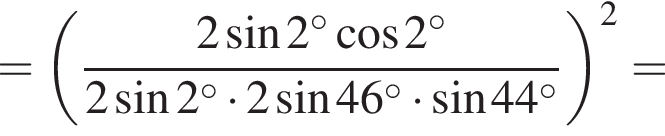
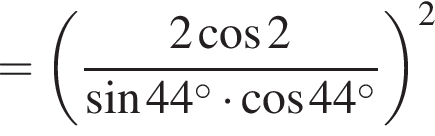
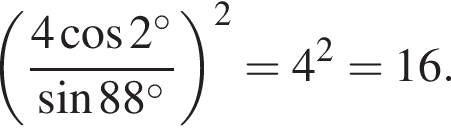
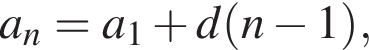 где d — разность арифметической прогрессии.
где d — разность арифметической прогрессии. 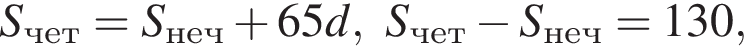 откуда
откуда 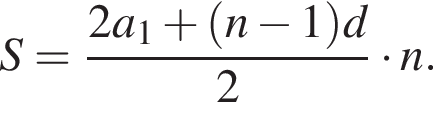 Следовательно, согласно условию, имеем:
Следовательно, согласно условию, имеем: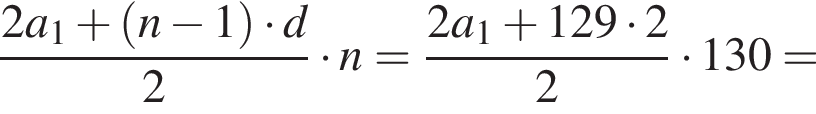
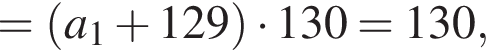
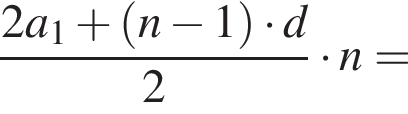
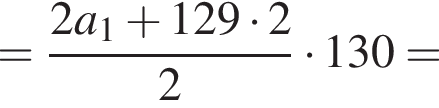
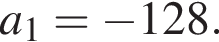 Получим
Получим 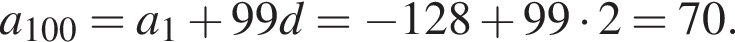
 Поскольку все стороны трапеции, кроме большего основания равны a, получим
Поскольку все стороны трапеции, кроме большего основания равны a, получим  Тогда
Тогда 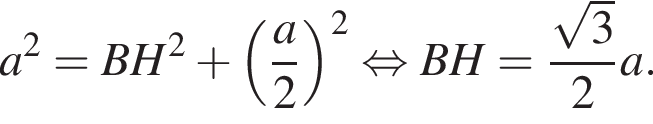

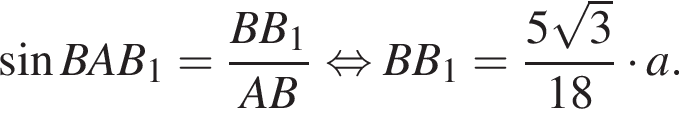
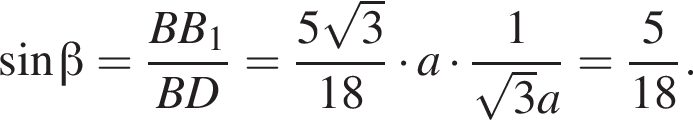
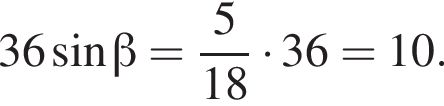
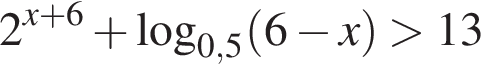 равно ...
равно ...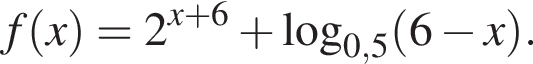 Заметим, что по смыслу задачи
Заметим, что по смыслу задачи 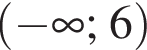
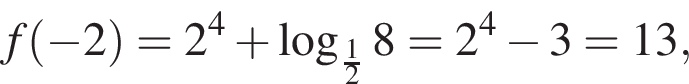 неравенство верно для всех x из
неравенство верно для всех x из 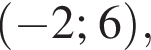 который содержит 7 целых чисел:
который содержит 7 целых чисел: 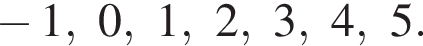
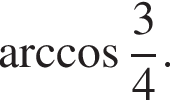 Ребро SD перпендикулярно основанию, а ребро SB образует с основанием угол
Ребро SD перпендикулярно основанию, а ребро SB образует с основанием угол 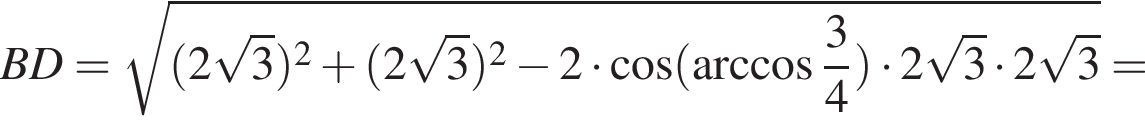
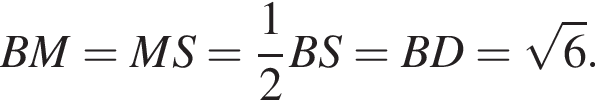
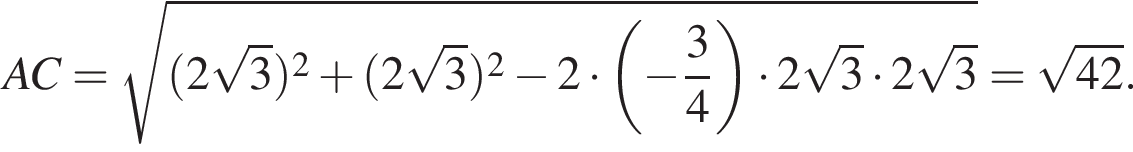
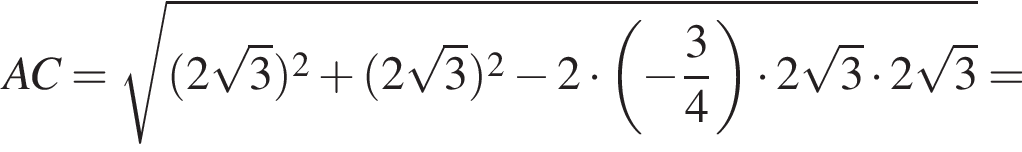

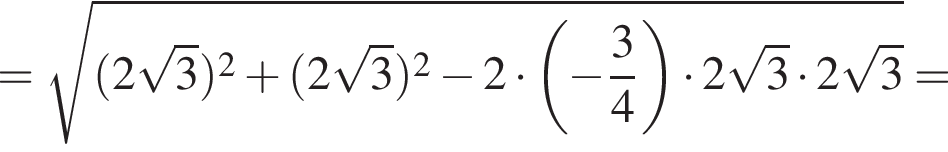
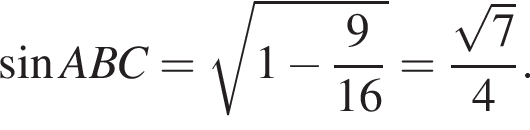
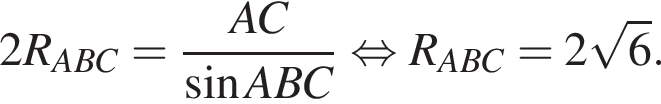
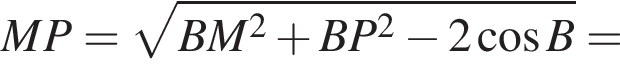
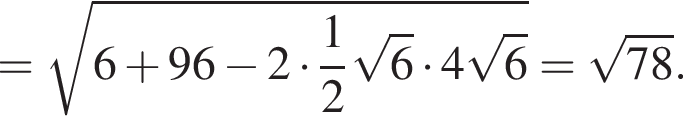
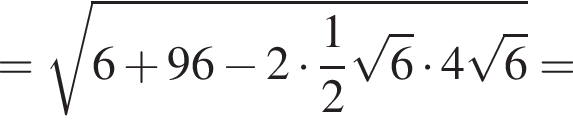


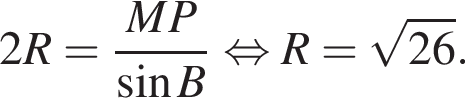 Таким образом,
Таким образом,